Gary Wysin, Condensed Matter Physics
Magnetism and Optics Theory and Simulation

The Beira Mar, Florianópolis, Santa Catarina, Brazil, 2005.
106 Cardwell Hall,
Department of Physics,
Kansas State University,
Manhattan KS 66506-2601, USA.
(785) 532-6786 / FAX: (785) 532-6806
Best way to contact me: wysin@ksu.edu
Curriculum Vita on the Lattes system in Brazil
Google Scholar Profile and Citations
ResearcherID Profile and Citations
Graduate Level Physics Books:
Statistical Thermodynamics: Understanding the Properties of Macroscopic Systems,
Lukong Cornelius Fai and Gary Matthew Wysin
Find it at Taylor & Francis, published October 2012
Find it at Amazon
Magnetic Excitations and Geometric Confinement: Theory and Simulations,
Gary Matthew Wysin
An Institute of Physics Expanding Physics ebook, published December 2015
Congratulations, however you did it, you found me! If you are interested in
theoretical physics, or in making computer simulations in physics, or just
want to know what I am doing, this is a good place to start.
There's an interesting world of magnetism, from the very applied, such as all
those MegaBytes of magnetic disk storage you are now using, to the very abstract, which
includes solitons and vortices. I use a combination of mathematical physics,
statistical physics, solid state physics, quantum mechanics, and common sense to figure out how
to get computers to calculate what I want to know about various magnetic materials.
It is all based on models of interacting spins on a lattice,
which are the microscopic magnetic moments (arrows) that can cooperate to
form what we see in magnetized objects, usually by all trying to be parallel.
What I do in physics:
Teaching:
Disclaimer: If you can't see any problem solutions for some class,
unfortunately I had to limit the access for one reason or another,
sorry!!! That way you will have more pleasure working the problems
out yourself!

- K-State Grad Physics
- Brief overview of our Graduate Physics program.
- Physical World I 101
- Introductory course on many topics in science, especially physics and chemistry.
Go here to see Review Questions and Problems and other Physical World I information.
- General Physics I Lecture 113
- 2007-present.
Motion, mechanics, energy, waves and thermodynamics.
Lecture notes and Exam solutions.
- General Physics II Lecture 114
- 2007-present.
Electricity, magnetism, optics, quantum and nuclear physics.
Lecture notes and Exam solutions.
- General Physics II Recitation 114
- Electricity, magnetism, and beyond.
Brief summaries of the concepts and formulas for important topics.
- Descriptive Astronomy 191
- Go here to see Review Questions and Problems
and other Introductory Astronomy information.
- Engineering Physics I Lecture/Studio 213/223
- Newton's Laws, thermodynamics, work, energy and all that.
Go here to see my scribblings of solved EPI physics problems,
and other EPI information.
- Engineering Physics II Lecture 214/224
- Electric and magnetic fields, circuits, optics.
Go here to see my EPII lecture notes and other information.
- Electromagnetic Fields I 532
- Undergraduate course on electric and magnetic fields,
statics and intro to Faraday's Law and Maxwell's equations.
Lecture notes.
- Applied Quantum Mechanics 709
- Overview of basic applications of quantum mechanics in
modern physics. Go here to see my lecture notes and other information.
- Physics Journal Club 806
-
Click to see the schedule of teaching and research talks that took place.
- Mathematical Methods for Physicists 801
- Advanced mathematical techniques for solving theoretical physics problems.
- Quantum Mechanics-I 811
- Graduate level quantum mechanics. Fundamentals, Schrodinger Eqn.,
wavefunctions, representations, etc.
- Quantum Mechanics-II 911
- Graduate level quantum mechanics. Scattering, spin, rotations, perturbation theory,
introduction to relativistic theory.
- Electrodynamics-I 831
-
Graduate level analysis/application of Maxwell's equations, advanced mathematical
techniques for elecrostatics, magnetostatics, time-dependent fields, electromagnetic waves.
- Electrodynamics-II 931
-
Graduate level analysis/application of Maxwell's equations for
electromagnetic radiation from antennas and moving particles,
relativistic EM fields.
- Statistical Mechanics 971
-
Graduate level analysis/applications of statistical physics and thermodyamics for classical and
quantum ideal gases, nonideal gases, superfluids, magnetism, phase transitions and critical properties.
- Statistical Thermodynamics: Understanding the Properties of Macroscopic Systems
- Description of book published by Taylor & Francis, October, 2012.
A graduate level text on thermodynamics and statistical mechanics with applications in classical and quantum statistics of
ideal gases, lattice dynamics, electron gas, dielectrics, magnetism, semiconductors, superfluids, functional integration and
path integrals.
Research:
Some short descriptions of recent and not-so-recent work.
- Publications
- My recent and not so recent papers, proceedings articles, and zipped RevTex preprints.
- Presentations
- Slide presentations of physics research.
- Optical Bistability with Surface Plasmons
- Master's Thesis, Gary M. Wysin, Department of Physics, University of Toldeo, 1980.
Oriented by R.T. Deck and H.J. Simon.
- Classical Kink Dynamics and Quantum Thermodynamics in
Easy-Plane Magnetic Chains with an Applied Magnetic Field
- Ph.D. Thesis, Gary M. Wysin, Department of Physics, Cornell University, 1985.
Oriented by J.A. Krumhansl and A.R. Bishop.
- Current and Past Funding
- My thanks to KSU, NSF, NSF-EpsCoR, NAS/NRC, CNPq and FAPEMIG for their support.
- Research Experiences for Undergraduates, Summer 2008
- Introductory information about a project on control of magnetic vortex properties.
- Physics Research Topics
- Some of the physics problems I've worked on, concerning vortices,
domain walls, fine magnetic particles, and their hysteresis.
- Computational Techniques and Simulations
- How some of the calculations are done, including Monte Carlo,
Spin Dynamics, and Numerical Diagonalization.
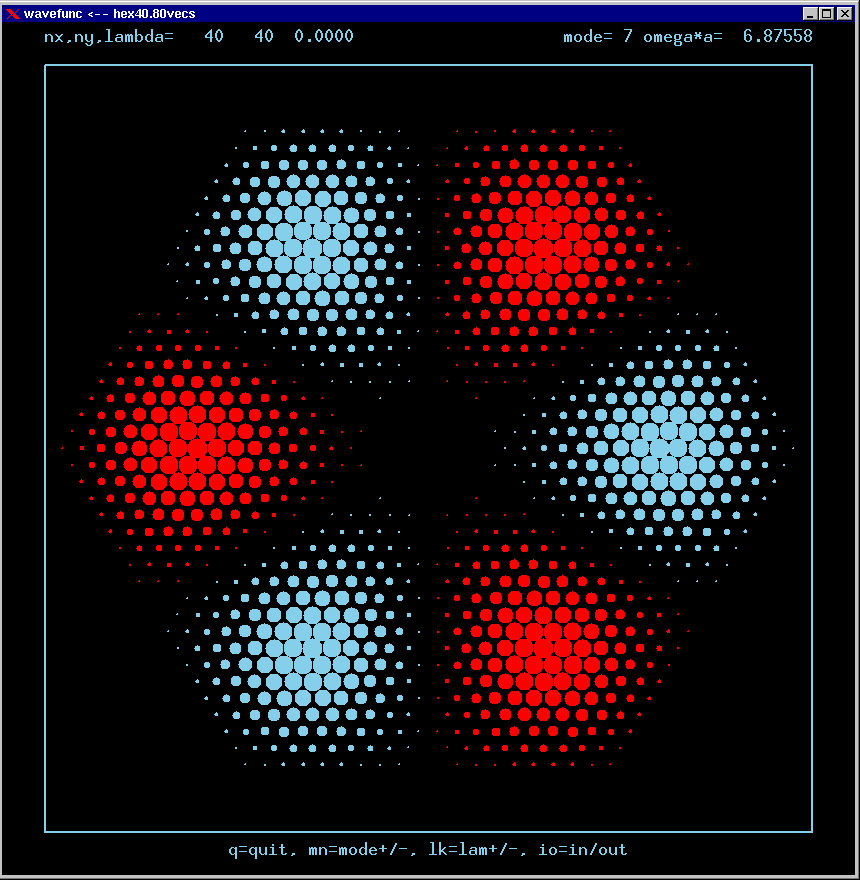
- Optical Modes in Micro-Cavities (see image -->)
- Diagrams of the vibrations of electromagnetic fields (or
elastic membranes like drums!) when constrained to occur within
equilateral triangles or hexagons. Nice wavefunction plots!
- Vortex-Spinwave Scattering Results
- Some technical notes on my calculations of the spectrum of
spinwaves in the presence of a magnetic vortex in two dimensions.
- Notes on Numerical Quantum Mechanics
- Some technical notes on recent Quantum Monte Carlo methods
for spin models.
Physics Notes:
Some notes on graduate level physics problems. These might be of interest to graduate students in
physics, chemistry, engineering and related fields. Knowledge of quantum mechanics, statistical
mechanics, and electrodynamics is assumed for most of these notes.
- Quantization of the Free Electromagnetic Field: Photons and Operators
- The main ideas and equations for quantized free electromagnetic fields are developed and summarized here,
based on the quantization procedure for coordinates (components of the vector potential A) and their canonically
conjugate momenta (components of the electric field E).
- Probability Current and Current Operators in Quantum Mechanics
- A quantum particle such as an electron produces electric current because of its motion. That current
is associated with the flow of its probability. The formalism to discuss quantum currents, in terms of
density matrix ideas, is discussed here.
- Quantum Theory for Dielectric Properties of Conductors
A. Response to Optical Electric Field Only
- The complex and frequency-dependent dielectric function ε(ω) describes how light interacts when
propagating through matter. Of particular interest here is the description of ε(ω) in conductors
using quantum mechanics, so that intrinsically quantum mechanical systems can be described. This part A leads
to a description of the contributions from band-to-band transitions, such as in metals and semiconductors.
- Quantum Theory for Dielectric Properties of Conductors
B. Magnetic Fields and Landau Levels
- In part B, the important problem is how to include the effect of a DC magnetic field in the
dielectric function, and describe how it causes Faraday rotation. One possible effect of the magnetic field
is that it produces quantized Landau levels for the eletrons. The dielectric function ε(ω)
for a free electron gas is found, using the Landau levels.
- Quantum Theory for Dielectric Properties of Conductors
C. Effects of Magnetic Fields on Band-To-Band Transitions
- In part C, the quantum effects of a DC magnetic field on the band-to-band transitions, such as
those in metals and semiconductors, are discussed. Results for ε(ω) are found for 1D and 3D
band models, with and without a phenomenolgical damping.
- Associated Legendre Functions & Dipole Transition Matrix Elements
- Notes on Legendre polynomials, associated Legendre functions, spherical harmonics, and the properties
needed from them to get electric dipole transition matrix elements. Possibly useful where a problem
involves electric dipole transitions and the matrix elements are desired.
- Stochastic Spin Dynamics & Langevin-Landau-Gilbert Simulations
- The dynamics of microscopic systems, primarily for spin models in thermal equilibrium is discussed,
where the temperature causes random forces or torques, which are in competition with a damping force.
This includes summarizing Langevin dynamics and finding methods for integrating the Landau-Gilbert equation
of micromagnetics in time, with damping and temperature.
- Demagnetization fields
- A discussion of the magnetic fields inside and around a magnet, that are caused by that magnet.
Mainly considers a permanent magnet of cylindrical shape. Also shows how to get effective Green's
functions for finding the magnetic field inside a very thin magnet with an arbitrary magnetization,
as would be needed in some micromagnetics simulations of thin-film magnets.
- Pythagorean Theorem Proofs
- No physics here. Just for fun, two simple and diferent proofs of the Pythagorean theorem for right
triangles, a2+b2=c2. If you have others, let me know!
Physics Graphics Simulations with C/X11-Programming
These are some visualization programs I wrote for physics fun. They are
great for seeing the dynamics in some simple systems.
You'll need a c-compiler, UNIX and X11 libraries to compile and run them.
See the first few lines of the main programs to get the compile command.
Hit the 'h' key to get a window showing the key-touch commands (click the
program images here to see that).
These should run on Linux, Apple, and other unix systems.
-
-
A UNIX c-program that quickly opens a window and draws plots of xy data
from data files given to it. It's a fast alternative to using gnuplot or
xvgr/xmgr. Hit 'h' for help window which shows all single keyboard stroke
commands. Includes 'p' and 'l' for portrait or landscape PostScript
printout.
Source code in C/X11 is here: xgrph.zip.
For a sample data file, click --> sample_data .
If you use it and find bugs please report them to me at wysin@phys.ksu.edu.
-
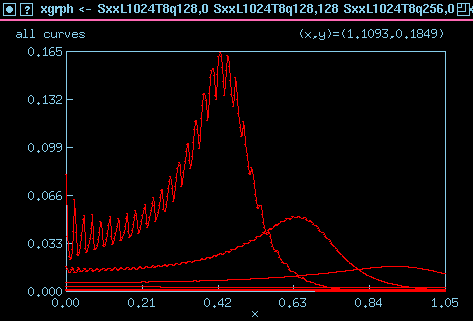
Typical graph drawn by xgrph with data for multiple curves inputted from
several files.
-
- A UNIX c-program that gives graphical demonstration of elliptical
planetary orbits. For C/X11 source code click here:
xorbit.c.
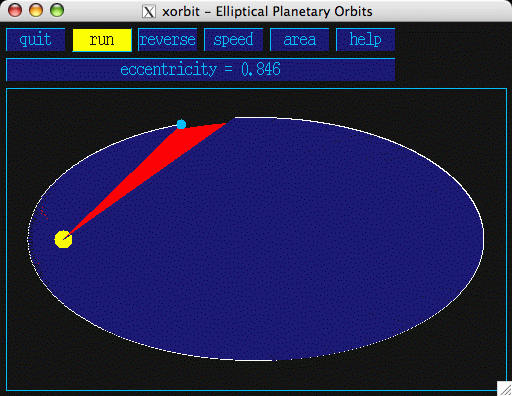
The radius from Sun to planet sweeps out equal areas in equal times, Kepler says.
-
- A UNIX c-program that simulates motion and collisions of a mixture of
2D balls, with gravity, time-reversal, and pressure and rms speed measurement.
For C/X11 source code click here:
gas2d.zip.
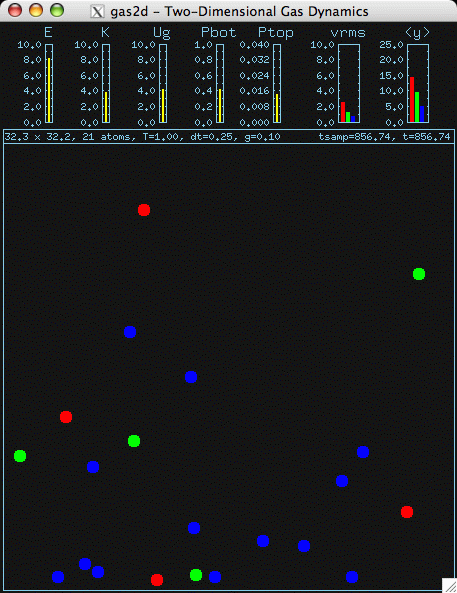
Light,
intermediate, and
heavy balls in thermal equilibrium in a
gravitational field, from gas2d simulation.
-
- A UNIX c-program that simulates a magnet made of 2D planar rotors under the
influence of temperature and applied magnetic field. It shows the magnetization changes,
using Metropolis Monte Carlo or Langevin spin dynamics. Made in collaboration
with the PhET project at University of Colorado ,
with support of a 2010 Big 12 Faculty Fellowship from Kansas State University.
See a short report on my Big 12 Fellowship activities.
The program source code is here:
rotor.zip (Planar-Rotor Magnet).
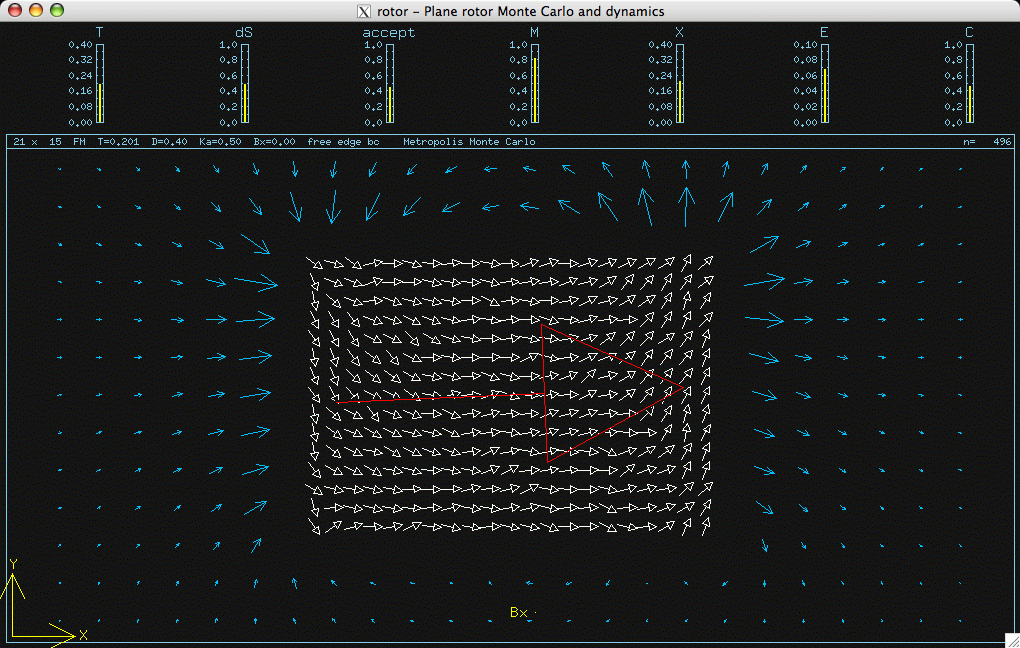
Planar rotor dipoles and the field they produce for a magnet at low temperature.
The large red arrow is the net magnetization. There is no applied field. The rotors
start to form domains, due to dipole-dipole interactions.
-
- A UNIX c-program that demonstrates how the spins and vortices in a magnet move around
under the influence of temperature only (xmc) or under temperature and time (xmd).
Source code is here:
xmc.zip (Monte Carlo with spin dynamics).
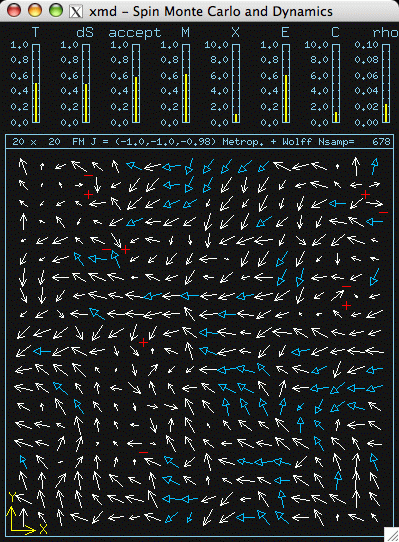
Simulation of anisotropic Heisenberg model near its critical temperature,
showing calculations of absolute magnetic moment in XY plane, susceptibility,
internal energy, specific heat, and vorticity density. Blue/white arrows
indicate spins with +/- components out of the XY plane. Red +/- indicate
vortices/antivortices.
Other Information:
- Co-workers on these projects
- It's a small world. These are some of the people I visit and work with.
- Physics photo album
- Interesting pics of our world.
- A local photo album
- My art work.
Physics Department:
Other Links At KSU:
[Error Creating Counter File]
since 2006/02/10.
Last update: Monday August 18 2025.
email to -->
wysin@phys.ksu.edu

GMW at the Konza Prairie, July 1995.








