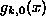 has a gapless
continuous spectrum only, with the usual oscillating asymptotic
scattering form far from the vortex,
has a gapless
continuous spectrum only, with the usual oscillating asymptotic
scattering form far from the vortex,
For m=0, the equations for f and g are uncoupled and have
the forms of usual Schrödinger equations (SE). Then it is easy
to show that the equation for 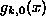 has a gapless
continuous spectrum only, with the usual oscillating asymptotic
scattering form far from the vortex,
has a gapless
continuous spectrum only, with the usual oscillating asymptotic
scattering form far from the vortex,
The equation for 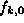 can be put in the form of a SE with
the potential
can be put in the form of a SE with
the potential 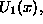 where
where 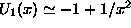 at
at 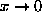 and
and 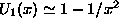 at
at 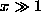 . So, the
continuous spectrum of this problem has a gap, and for
. So, the
continuous spectrum of this problem has a gap, and for 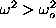 can be put in form (10) far from
the vortex, with
can be put in form (10) far from
the vortex, with 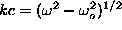 . But the
presence of the attractive part of the potential,
. But the
presence of the attractive part of the potential,
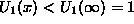 , gives the possibility of the appearance
of a local mode with the frequency
, gives the possibility of the appearance
of a local mode with the frequency
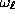 ,
, 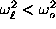 , with
well-pronounced exponential decay,
, with
well-pronounced exponential decay, 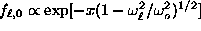 . The analysis of this
mode was done numerically by using a shooting
method[15] in finite circular systems of radius
. The analysis of this
mode was done numerically by using a shooting
method[15] in finite circular systems of radius
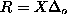 , with the conditions,
, with the conditions, 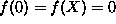 ,
, 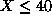 . Comparison with the results of exact diagonalization
have shown very good agreement of the two approaches, see
Fig. 3. The dependence of
. Comparison with the results of exact diagonalization
have shown very good agreement of the two approaches, see
Fig. 3. The dependence of 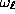 on R is
very weak for large enough R, e.g.,
on R is
very weak for large enough R, e.g.,
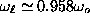 for
for 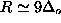 , and
, and
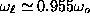 for
for 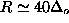 .
Size effects become strong only for
.
Size effects become strong only for
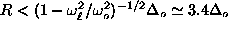 .
The presence of a literally local mode inside the
continuous spectrum is a unique property of AFM-vortices.
It should manifest itself in response functions of the AFM's with
vortices, and since the excitation of the local mode
requires no momentum transfer, such resonance can in
principle be observed in ESR experiments.
.
The presence of a literally local mode inside the
continuous spectrum is a unique property of AFM-vortices.
It should manifest itself in response functions of the AFM's with
vortices, and since the excitation of the local mode
requires no momentum transfer, such resonance can in
principle be observed in ESR experiments.