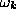 for
for 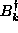 ) for the
two different boundary conditions are shown in Fig. 3 for a 180 site
system. For both types of boundary conditions in Fig. 3,
out-of-plane spin components are present in the static vortex for
) for the
two different boundary conditions are shown in Fig. 3 for a 180 site
system. For both types of boundary conditions in Fig. 3,
out-of-plane spin components are present in the static vortex for 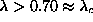 .
.
Some typical spectra (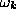 for
for 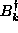 ) for the
two different boundary conditions are shown in Fig. 3 for a 180 site
system. For both types of boundary conditions in Fig. 3,
out-of-plane spin components are present in the static vortex for
) for the
two different boundary conditions are shown in Fig. 3 for a 180 site
system. For both types of boundary conditions in Fig. 3,
out-of-plane spin components are present in the static vortex for 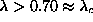 .
.
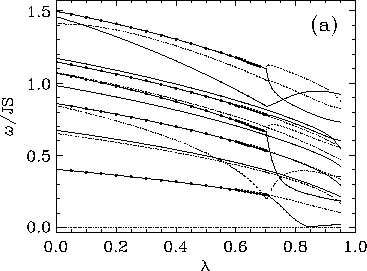
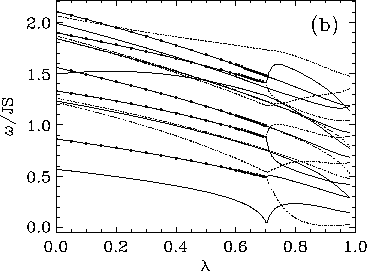
Figure 3:
Comparison of the lowest 19 modes in the spinwave spectrum
for a square lattice circular system with 180 sites, containing an in-plane vortex at
its center, with (a) free boundary conditions, and (b) fixed boundary
conditions. Degenerate modes are marked with solid circles.
The solid and dotted lines are used only to distinguish nearby modes.
There are some striking features of these results, which are typical of all the
eigenspectrum results for different sized systems and lattices. Consider the
fixed boundary condition (Fig. 3b). One mode of the in-plane vortex
(the lowest mode) comes close to zero frequency as 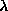 approaches
approaches 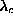 from below. This mode is still present for
from below. This mode is still present for 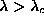 , with the out-of-plane vortex as static structure, and its
frequency again rises away from zero. The spectrum suggests that this mode can
be considered as a soft mode that is responsible for the energetic instability
of an in-plane vortex to become an out-of-plane vortex, and vice-versa, as
, with the out-of-plane vortex as static structure, and its
frequency again rises away from zero. The spectrum suggests that this mode can
be considered as a soft mode that is responsible for the energetic instability
of an in-plane vortex to become an out-of-plane vortex, and vice-versa, as
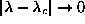 . The other obvious feature of the
spectrum is that modes that are degenerate (solid circles) for the in-plane
vortex become split for the out-of-plane vortex. This change also occurs for
. The other obvious feature of the
spectrum is that modes that are degenerate (solid circles) for the in-plane
vortex become split for the out-of-plane vortex. This change also occurs for
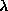 near
near 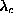 . It is likely that the degeneracy for
. It is likely that the degeneracy for
 for the in-plane vortex comes about because these modes
have an
for the in-plane vortex comes about because these modes
have an 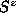 component that can be essentially ``up'' or ``'down''. On the
other hand, for the out-of-plane vortex, this up-down symmetry is certainly
violated, because the static spin configuration already possesses a nonzero
component that can be essentially ``up'' or ``'down''. On the
other hand, for the out-of-plane vortex, this up-down symmetry is certainly
violated, because the static spin configuration already possesses a nonzero
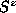 profile. Also, one of the modes that comes out of the lowest
degenerate pair goes very close to zero frequency for
profile. Also, one of the modes that comes out of the lowest
degenerate pair goes very close to zero frequency for 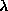 near 0.9 .
near 0.9 .
There are some differences for the free boundary condition, Fig.
3a. Here the ``soft mode'' that bears the most resemblance to that
for the fixed boundary condition reaches a downward cusp at 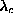 , but
does not go below
, but
does not go below 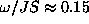 . On the other hand, this is the
value of
. On the other hand, this is the
value of 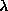 above which the lowest degenerate mode becomes
nondegenerate, one component of which does go very close to zero
frequency near
above which the lowest degenerate mode becomes
nondegenerate, one component of which does go very close to zero
frequency near 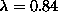 , and then rises up again. For both boundary
conditions, there are actually several modes higher up in the spectra that also
come to downward cusps near
, and then rises up again. For both boundary
conditions, there are actually several modes higher up in the spectra that also
come to downward cusps near 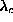 , while other modes show no particular
features near
, while other modes show no particular
features near 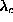 .
.