The process of isomerization, where one form of a molecule rearranges into another, is an important concept in physics and chemistry. One of the simplest examples is C₂H₂, which has two isomers: acetylene and vinylidene. While the isomerization of the neutral molecule has been extensively studied, much less is known about the behavior of its ionic forms. This summer, my project focused on understanding how this reaction changes when C₂H₂ is ionized, with the goal of uncovering broader trends in its isomerization behavior.

I approached the project in three stages. First, I computed potential energy surfaces for the reaction (which can be seen in figure 1). Next, I optimized several computational parameters, including the choice of basis set and active space, for both acetylene and vinylidene at different geometries. Finally, I attempted to compute intrinsic reaction coordinate (IRC) curves for the C₂H₂ cation, which trace the minimum-energy pathway between isomers.

Fig. 1: Potential curves of the four charged states of C₂H₂ I investigated this summer. Computed at the MCSCF level of theory with a (6,10) active space, and the AVTZ basis set.

 

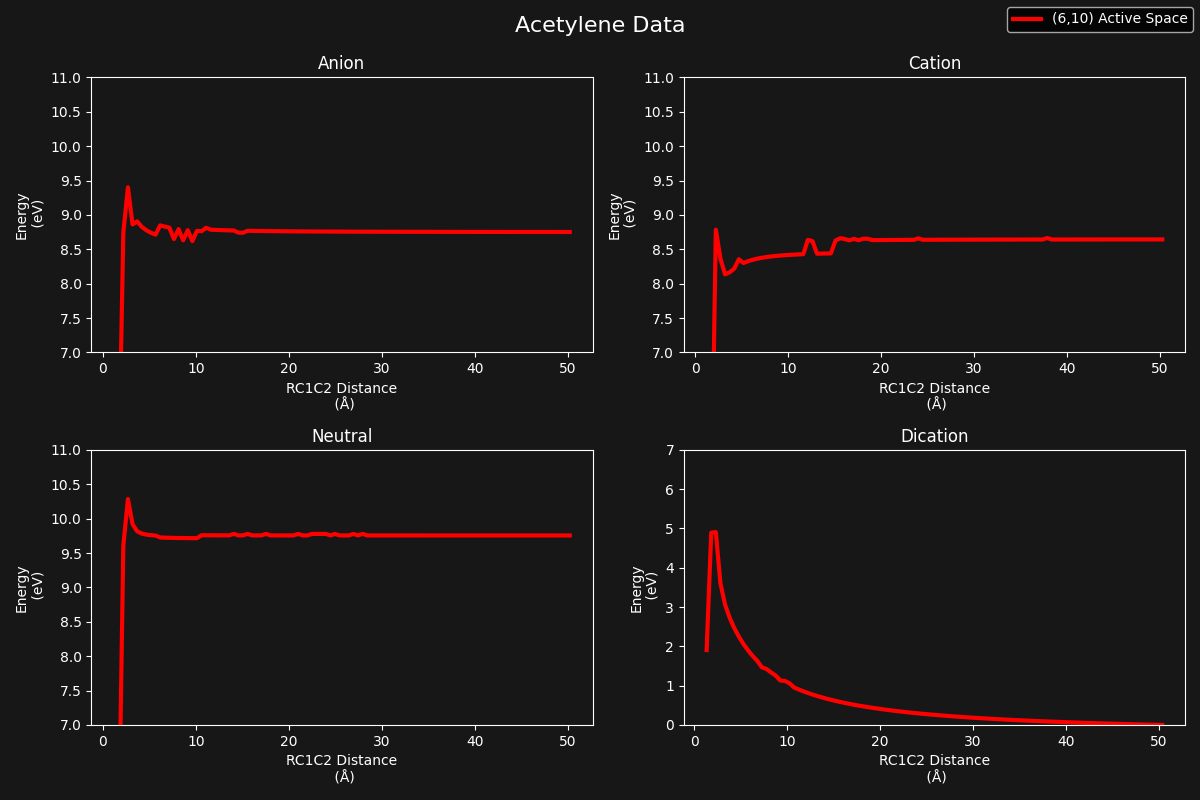
To perform these computations, I used the quantum chemistry software Molpro. Because of the computational complexity involved—particularly for multireference methods and geometry scans—I ran many of the calculations in parallel on the Beocat High-Performance Computing Cluster (HPC cluster).

While I successfully computed the potential energy surfaces and optimized parameters, the IRC calculations encountered challenges. Specifically, I had difficulty locating a viable transition state from which to begin the IRC, likely due to the complexity of the potential surface in that region. Future work could focus on mapping the surface more closely near the expected transition state to improve convergence and enable a complete IRC pathway for the C₂H₂ Cation.

Acknowledgments
I would like to thank Dr. Loren Greenman and Joshua Stallbaumer for their mentorship and support throughout this project, as well as the rest of Dr. Greenmans group. I am also grateful to the K-State REU program directors, Dr. Loren Greenman and Dr. Bret Flanders, as well as Kim Coy, for organizing and facilitating this valuable research experience. This work was supported by the National Science Foundation under Award No. 2244539. The computations for this project were performed on the Beocat Research Cluster at Kansas State University, which is funded in part by NSF grants CNS-1006860, EPS-1006860, EPS-0919443, ACI-1440548, CHE-1726332, and NIH grant P20GM113109. I also extend my thanks to Kansas State University for hosting the REU program and providing the resources that made this research possible.

Final Presentation