In AMO, we want to take pictures of molecules. One way to accomplish this is through the use of Laser Induced Electron Diffraction (LIED). To take good pictures using LIED, we need a laser suitable for LIED. That means it must be three things.

1. Pulsed: In order to ionize the molecule.

2. High repetition: In order to take large amounts of data quickly.

3. Mid-IR (3-4um): For reasons I'll get into later

One thing our group is aiming to accomplish with this laser is to differentiate between two isomers of butane: n-butane and isobutane. The ball and stick models for these two molecules (Fig. 1) look very different from each other. However, down on the atomic level, their Differential Cross Sections (DCS)—analogous to how they look to the probing electron—appear nearly identical (Fig. 2). To see a distinct difference between the two DCS, very large amounts of high-quality statistics are needed. Previous experiments have tried to distinguish between them using a 3um, 1kHz pulse laser. However, these experiments did not have enough data for them to be conclusive. Our current laser is 100kHz, but we can’t take useful data with it because the wavelength is 1um. So, we need to increase it to 3um. First, for background, I’ll talk about our experimental setup and how we take data before explaining why we want a mid-IR laser and how we achieved it.

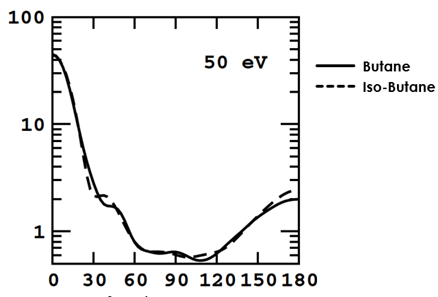Fig. 1. DCS of Butane Isomers
Source: Lopes et al. (2004)

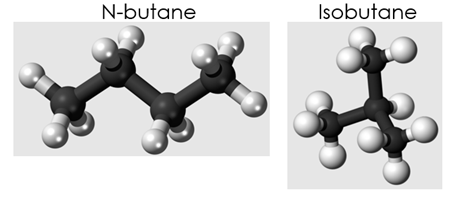Fig. 2. Butane Isomers

The beam we use is a 1um, 100kHz pulse laser (2 of the 3 things we want). As you can see in Fig. 3, we first take the beam and propagate it into the center of our TOF chamber, where it gets focused to the interaction region in the middle for ionization to occur. The chamber is hooked up to a vacuum system to isolate the gas sample from outside contaminants, and then the gas sample is pumped inside. The chamber is made to be field-free, so that when calculating the kinetic energy of electrons, we don’t need to account for any external fields. The chamber has 2 micro channel plate (MCP) detectors, so that when an electron hits it, the electric signal gets amplified manyfold and is detected as a hit. I also helped prep the chamber by baking it—a process to lower the internal pressure—so the chamber is now ready to take data during our next beam time.

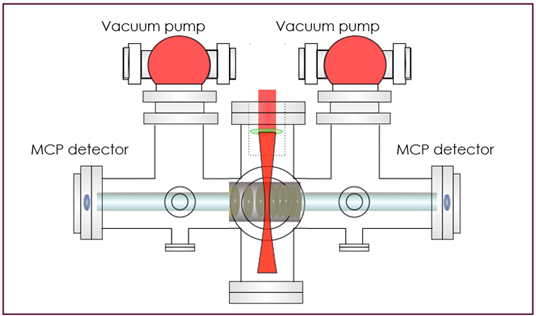Fig. 3. TOF Chamber

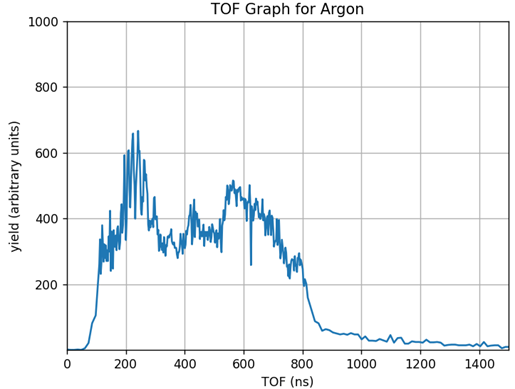
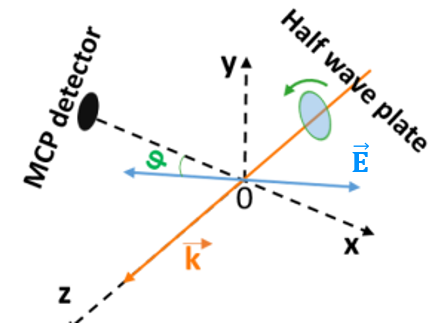
Next, we take time of flight (TOF) measurements. We measure how long it takes the electron to reach the detector after being ionized. We do this for every pulse, and, at 100kHz, we quickly get something that looks like Fig. 4. This TOF graph shows the number of electrons seen at different electron flight times. Then, we do the experiment again, but change the polarization of the light using a half wave plate as seen in Fig. 5. This creates an angle of polarization—the angular difference between the electric field of the laser and the axis of our detector. We take TOF measurements at many different angles of polarization, and these TOF measurements at a range of angles serves as our raw data.

Fig. 4. TOF graph for argon

Fig. 5. TOF setup

Source: Zavareh, S. (2025)

Now that I’ve given some background, I’ll talk about why we need a higher wavelength. Some of the approximations we make for our theoretical model are only valid when the returning electron has high enough energy (at least 50eV). The 1um laser we are using does not achieve this. Return energy is proportional to laser intensity * . So, to increase our return energy, we need to increase one of these two values. Intensity can only be increased to a certain limit, because at some point it starts to ionize too many molecules at once. So, what we need to do is increase our wavelength. To accomplish this, we need to build an OPA.

Lasers have a certain wavelength, and we can make them produce different wavelengths with an optical parametric amplifier (OPA). In our case, we want to turn 1um into 3um. The primary process behind an OPA is difference frequency generation (DFG). In DFG, a pump—the laser source—is combined with a signal—a higher wavelength light—in a nonlinear crystal (Fig. 6). Through DFG, the signal is amplified and another light—the idler—is created. What’s happening can be explained with Fig. 7. The pump photon is split into two photons: the signal, and a photon with a frequency equal to the difference between the pump and signal, which we call the idler.

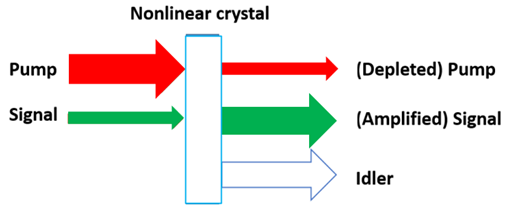Fig. 6. DFG through nonlinear crystal

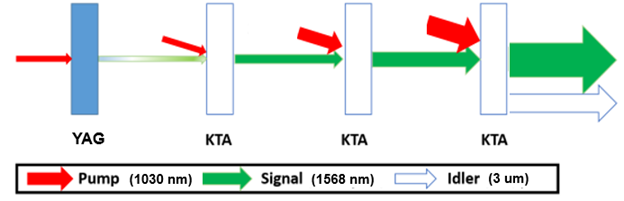Fig. 7. DFG process

 

Next, I will walk you through the setup of our OPA as shown in Fig. 8. First, the pump is divided into four different paths for use at various points in the process. In the first path, the pump passes through a YAG crystal, resulting in white light generation (WLG), which produces a broad spectrum of wavelengths. An important detail I neglected to mention earlier is that a KTA crystal can be rotated so that only a specific wavelength is amplified. By rotating this first KTA crystal, we can amplify the desired signal—1568nm. The KTA crystal is a nonlinear crystal, so besides amplifying the signal, it also generates an idler. For now, we only focus on the signal, so we block the idler and continue using the signal. The signal is amplified a second time with another branch of the pump, then amplified again for a third time. In this third path, we keep the idler, since it is the wavelength we want—3um—and block the signal. We now have our 3um beam! It is ready to be propagated to the chamber and used in experiments.

Fig. 8. OPA setup

Source: Zavareh, S. (2025)

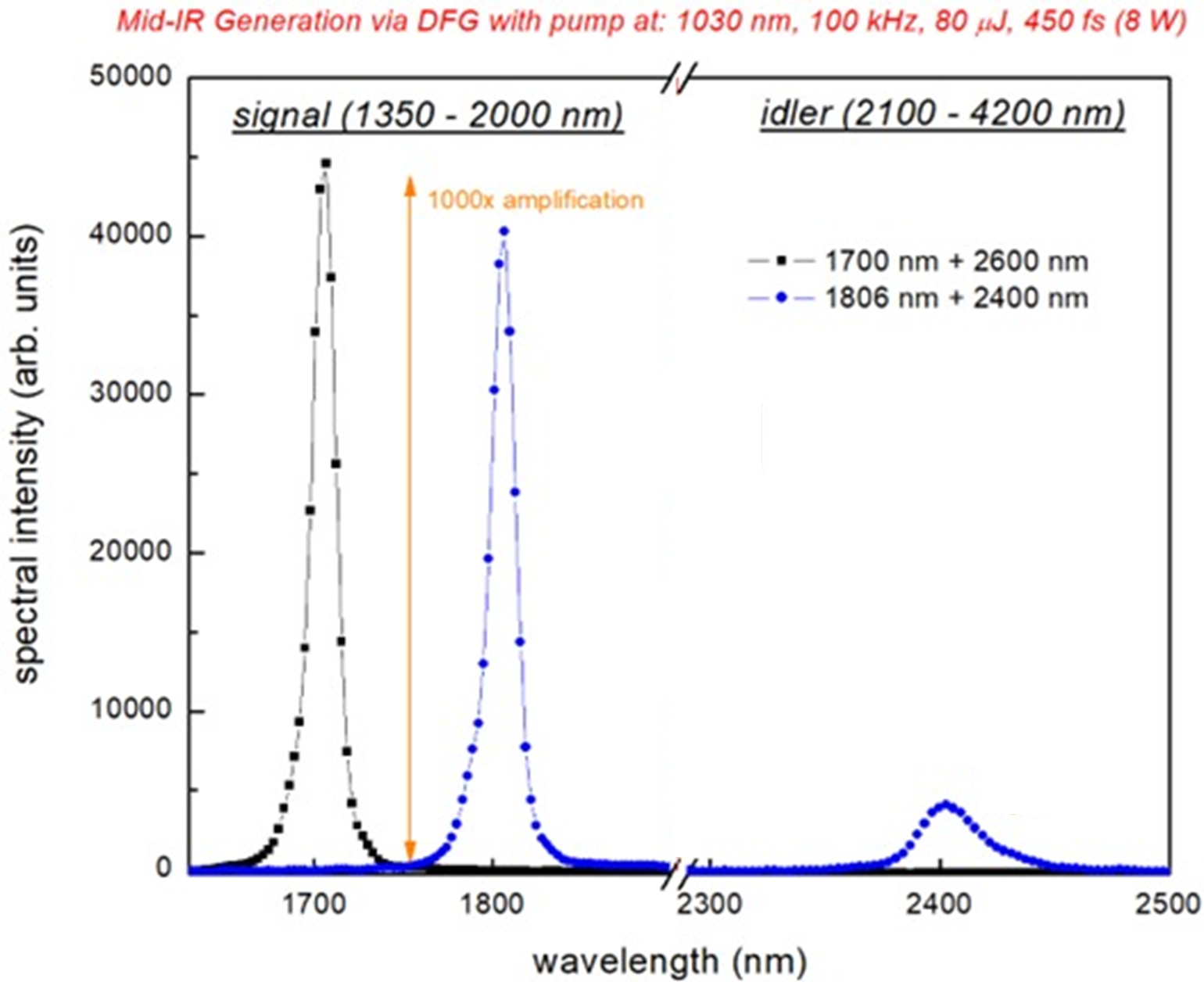
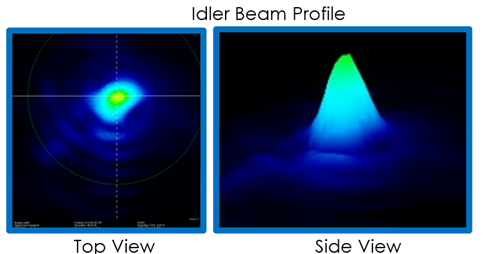
The finished OPA can be seen in Fig. 9. We were successful in creating our 3um beam. Our spectrometer only measures up to 2500nm, so we are not able to measure the wavelength directly. Fig. 10 shows a spectrogram taken after the first KTA crystal. We rotated the crystal, changing the signal to 1806nm and saw its corresponding idler at 2400nm, so we know that DFG is occurring. It’s not on this graph, but we also measured a 1.5um beam, which corresponds to a 3um idler. The 3um beam has an excellent beam profile (Fig. 11) and has an output of 250uJ/pulse, which we will focus and expect to generate an intensity of >50TW/cm2 inside the chamber. One aspect about the OPA I would like to emphasize is that the wavelengths output are adjustable. Looking at Fig. 10 again, you can see the range of the signal is 1350-2000nm with a corresponding idler range of 2100-4200nm. So, we are able to create and use a laser with a wavelength from 1350-4200nm, allowing us to perform a variety of different experiments, not just LIED.

Fig. 9. Finished OPA

Fig. 10.Spectrogram after first KTA crystal

So, we now have a laser that is suitable for LIED. It is pulsed—allowing us to ionize the molecule—high repetition (100kHz)—letting us take large amounts of data quickly—and mid-IR (3-4um)—so that we can use our theoretical model with valid approximations. Our laser wavelength is also adjustable, so if we want to study other phenomena with a specific IR wavelength needed, we have a way to do so. For our next step, we plan to retake data to differentiate between butane isomers. Our past data was taken at 1kHz, so we didn’t have enough data to be conclusive, but with our new 100kHz laser, we plan to take a surplus of data.

Fig. 11. 3um beam profile

Acknowledgments
I would like to thank my PI, Dr. Cosmin Blaga, and the rest of my group: Sajed Zavareh, Eric Mullins, Maggie Liu, Diksha Ahlawat, Frank Genty, and Lily Richard. I’d also like to thank everyone else who gave me advice and mentorship throughout the REU, as well as the JRM lab. I’d like to thank Kim Coy, Bret Flanders, Loren Greenman, and the rest of the K-State physics department for putting on the REU and providing me with this experience, as well as the NSF for sponsoring it. This material is based upon work supported by the National Science Foundation under Grant No. 2244539. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

Final Presentation