


Next: Effect of Vortex
Up: NORMAL MODES OF VORTICES
Previous: RESULTS: TRIANGULAR AND
Through numerical diagonalization of the spin equations of motion linearized about
a non-uniformly magnetized state, we have found the spinwave spectrum for finite
circular systems containing a single vortex at the center. The spectrum shows
some important dynamical properties of individual magnetic vortices. The most significant
feature is the presence of a particular mode [mode (a) in the Figures] whose frequency
comes close to zero near 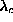 , and whose rms radius comes close to one lattice
constant at the same time. For
, and whose rms radius comes close to one lattice
constant at the same time. For 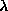 just below
just below 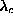 , such a localized mode
has a time-dependent spin structure with radial dependence of its amplitude very similar
to the static out-of-plane vortex structure present for
, such a localized mode
has a time-dependent spin structure with radial dependence of its amplitude very similar
to the static out-of-plane vortex structure present for 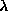 just above
just above
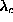 . This is suggested by comparing the mode (a) in Fig. 8 and the
lowest curve (
. This is suggested by comparing the mode (a) in Fig. 8 and the
lowest curve (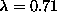 ) in Fig. 1. Thus, this mode is the precursor
to the instability of an in-plane vortex to become an out-of-plane vortex. This
idea is further supported by the fact that the rms radius of mode (a) becomes
comparable to the ``vortex core'' radius of an out-of-plane vortex for
) in Fig. 1. Thus, this mode is the precursor
to the instability of an in-plane vortex to become an out-of-plane vortex. This
idea is further supported by the fact that the rms radius of mode (a) becomes
comparable to the ``vortex core'' radius of an out-of-plane vortex for 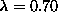 ,
defined by, [8]
,
defined by, [8]

On the other hand, for 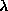 far below
far below 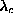 , mode (a) bears a lot of
similarity to the lowest mode when there is no vortex present. This can be
seen by comparing Fig. 7a and Fig. 10a. However, in the
absence of the vortex, this lowest mode undergoes no substantial changes as
, mode (a) bears a lot of
similarity to the lowest mode when there is no vortex present. This can be
seen by comparing Fig. 7a and Fig. 10a. However, in the
absence of the vortex, this lowest mode undergoes no substantial changes as
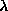 is increased, even through
is increased, even through 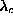 .
.
Gary M Wysin
Mon Sep 11 12:02:10 CDT 1995
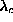 , and whose rms radius comes close to one lattice
constant at the same time. For
, and whose rms radius comes close to one lattice
constant at the same time. For 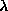 just below
just below 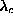 , such a localized mode
has a time-dependent spin structure with radial dependence of its amplitude very similar
to the static out-of-plane vortex structure present for
, such a localized mode
has a time-dependent spin structure with radial dependence of its amplitude very similar
to the static out-of-plane vortex structure present for 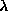 just above
just above
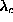 . This is suggested by comparing the mode (a) in Fig. 8 and the
lowest curve (
. This is suggested by comparing the mode (a) in Fig. 8 and the
lowest curve (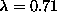 ) in Fig. 1. Thus, this mode is the precursor
to the instability of an in-plane vortex to become an out-of-plane vortex. This
idea is further supported by the fact that the rms radius of mode (a) becomes
comparable to the ``vortex core'' radius of an out-of-plane vortex for
) in Fig. 1. Thus, this mode is the precursor
to the instability of an in-plane vortex to become an out-of-plane vortex. This
idea is further supported by the fact that the rms radius of mode (a) becomes
comparable to the ``vortex core'' radius of an out-of-plane vortex for 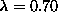 ,
defined by, [8]
,
defined by, [8]

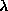 far below
far below 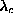 , mode (a) bears a lot of
similarity to the lowest mode when there is no vortex present. This can be
seen by comparing Fig.
, mode (a) bears a lot of
similarity to the lowest mode when there is no vortex present. This can be
seen by comparing Fig. 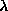 is increased, even through
is increased, even through 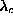 .
.